The Spiral of Theodorus

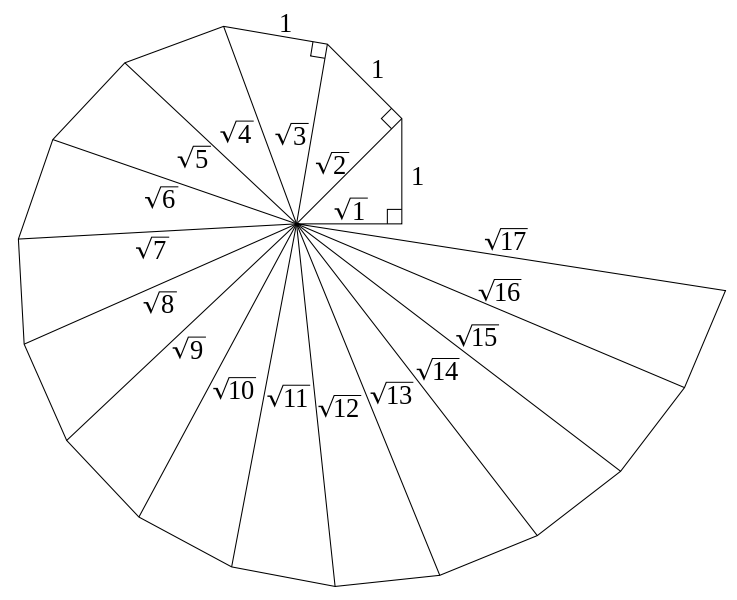
In Plato’s dialogue, Theaetetus (p. 147d), there is a cryptic description of a complicated geometrical diagram that the geometrician, Theodorus, drew for his students. Down through the centuries there has been much speculation about exactly what Theodorus was supposed to have drawn.

We know that it involved the roots of square areas in the natural number series up the area of 17, and so √17. But then at √17 Theodorus stopped, so we are told, because after that the diagram got ‘entangled’ (enescheto).

What happened after √17?

One answer to the riddle is now sometimes called the Spiral of Theodorus. When we drew this ‘root spiral’ in Geometry class on Tuesday night, we found that √17 was the last root that can be drawn before the spiral completes the circle and so becomes entangled.

If this were what Plato was hinting at, then it provides insight into how Plato and his contemporaries were dealing with geometric ratios that cannot be expressed arithmetically, that is, not as any finite fraction. As we would now say, such ‘surds’ can only be expressed arithmetically as approximations, like for √2 as 1.4, or, more precisely, as 1.4142857.

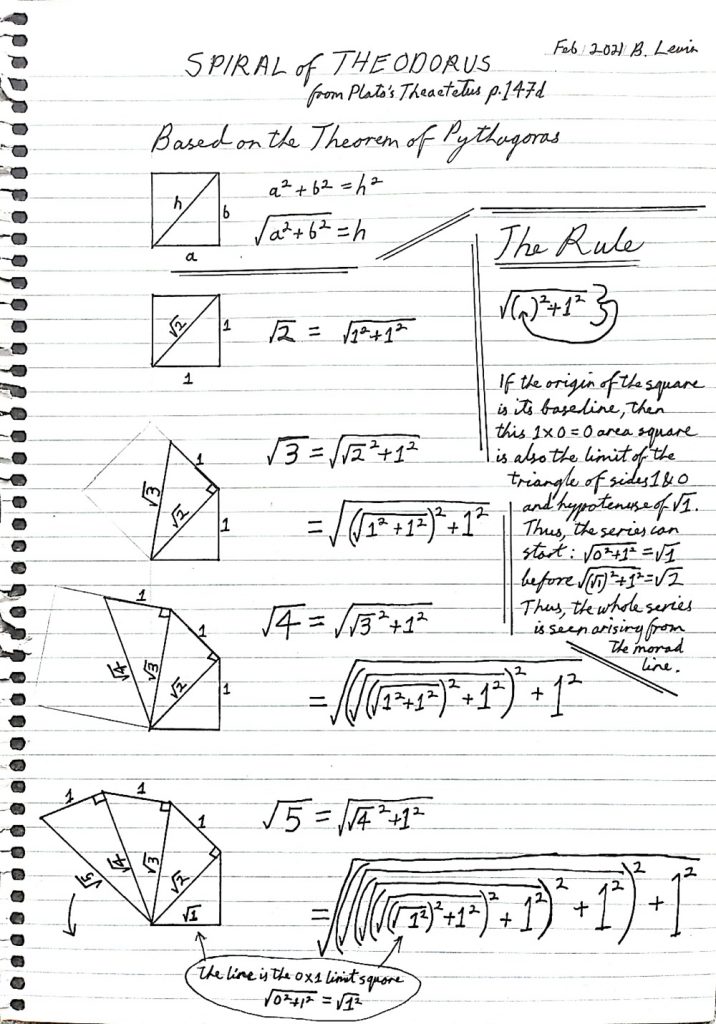
Of course, these roots remain perfectly presented geometrically. What is special about this spiral is that they are presented orderly in symmetrical relations to each other. This is affected by cutting off one side of the square at length 1 to make a triangle with the other side, and then using its hypotenuse (or ‘diagonal’) as the side (or ‘root’) of the next square…and then repeating this process over and over.

So, starting with the unit square (or ‘monad’ square), its diagonal √2 becomes the side of the next square of area 2. Then cut one side of this square off at 1 to make sides √2 and 1 of a new triangle by drawing in the hypotenuse, which – according to Pythagoras’ Theorem – measures √3. This hypotenuse is then taken as the root side of a new square of area 3, from which a new triangle is generated by cutting one side off at 1 to make a new triangle with sides 1, √3 and hypotenuse calculated as √4. And so on to √5, √6, √7…the spiral builds the successive roots according to the natural number series.

The notes below show the recursive rule for building the spiral as expressed in notation. By following the rule in the notation, we can see that the root series in the spiral is a fractal built from the unit square with area and root both 1. And so, the Spiral of Theodorus seems to be showing all roots of whole number squares emanating from – and so symmetrical with – the original monad square according to this simple recursive rule.